Contents
Custom Widget
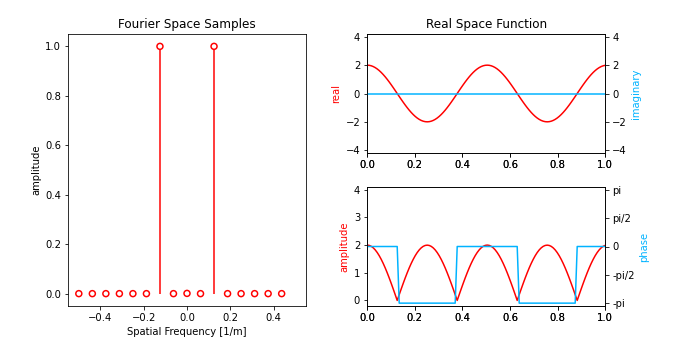
This is an example widget for more complicated interactive visualizations.
# Widget illustrating custom visualizations.
%matplotlib widget
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import display
from ipywidgets import HBox, VBox, Dropdown, Layout, Label, Output, widgets
from matplotlib import cm
dpi = 72
plt.close()
class FourierTransform1D:
"""
This class calculates and draws the 1D Fourier examples. Overall plot layout:
left -Fourier space, interactive scatter plot
right top -Real space, real/imag plotting, non-interative
right bottom -Real space, real/imag plotting, non-interative
Args:
f (np.array): numpy vector containing Fourier space representation of the function.
"""
def __init__(
self,
f = np.zeros(32),
):
# Figure layout
self.fig = plt.figure(figsize=(680/dpi, 340/dpi), dpi=dpi)
self.ax_FFT = self.fig.add_axes([0.1, 0.1, 0.35, 0.8])
self.ax_real = self.fig.add_axes([0.54, 0.55, 0.35, 0.35])
self.ax_imag = self.fig.add_axes([0.54, 0.55, 0.35, 0.35])
self.ax_abs = self.fig.add_axes([0.54, 0.1, 0.35, 0.35])
self.ax_phase = self.fig.add_axes([0.54, 0.1, 0.35, 0.35])
# axes limits, labels
self.ax_FFT.set_xlim([-0.55, 0.55])
self.ax_FFT.set_ylim([-0.05,1.05])
self.ax_FFT.set_xlabel('Spatial Frequency [1/m]')
self.ax_FFT.set_title('Fourier Space Samples')
self.ax_FFT.set_ylabel('amplitude')
self.ax_real.set_xlim([0.0,1.0])
self.ax_real.set_ylim([-4.2,4.2])
self.ax_real.set_title('Real Space Function')
self.ax_real.set_ylabel('real', color=(1,0,0,1))
self.ax_real.patch.set_alpha(0.0)
self.ax_imag.set_xlim([0.0,1.0])
self.ax_imag.set_ylim([-4.2,4.2])
self.ax_imag.yaxis.tick_right()
self.ax_imag.yaxis.set_label_position('right')
self.ax_imag.set_ylabel('imaginary', color=(0,0.7,1.0,1))
self.ax_imag.patch.set_alpha(0.0)
self.ax_abs.set_xlim([0.0,1])
self.ax_abs.set_ylim([-0.2,4.1])
self.ax_abs.set_ylabel('amplitude', color=(1,0,0,1))
self.ax_abs.patch.set_alpha(0.0)
self.ax_phase.set_xlim([0.0,1.0])
self.ax_phase.set_ylim([-3.3,3.3])
self.ax_phase.yaxis.tick_right()
self.ax_phase.yaxis.set_label_position('right')
self.ax_phase.set_ylabel('phase', color=(0,0.7,1.0,1))
self.ax_phase.set_yticks((
-np.pi,
-np.pi/2,
0.0,
np.pi/2,
np.pi,
))
self.ax_phase.set_yticklabels((
'-pi',
'-pi/2',
'0',
'pi/2',
'pi',
))
self.ax_phase.patch.set_alpha(0.0)
# Calculate plotting functions
self.calc_inv_transform(f)
# FFT plots
mag = np.abs(self.f)
phase = np.angle(self.f)
phase_c = cm.hsv(np.mod(phase/(2*np.pi),1.0))
self.p = self.ax_FFT.scatter(
self.q,
mag,
marker='o',
facecolors=(1,1,1,1),
edgecolors=phase_c,
linewidth=1.5,
zorder=4,
)
self.p_lines = self.ax_FFT.vlines(
self.q,
ymin=np.zeros_like(self.q),
ymax=mag,
color=phase_c,
linewidth=1.5,
)
# real / imag plots
self.p_real = self.ax_real.plot(
self.r,
self.f_real,
color=(1,0,0,1),
linewidth=1.5,
)
self.p_imag = self.ax_imag.plot(
self.r,
self.f_imag,
c=(0,0.7,1.0,1),
linewidth=1.5,
)
# abs / phase plots
self.p_abs = self.ax_abs.plot(
self.r,
self.f_abs,
color=(1,0,0,1),
linewidth=1.5,
)
self.p_phase = self.ax_phase.plot(
self.r,
self.f_phase,
c=(0,0.7,1.0,1),
linewidth=1.5,
)
def calc_inv_transform(
self,
f,
upsample_factor = 8,
):
"""
This function calculates the inverse Fourier transform of a function,
zero-padding it to Fourier upsample the real space result.
It saves all values (including coordinate vectors for plotting) locally.
"""
# Fourier space
self.f = np.array(f,dtype='complex')
self.q = np.fft.fftfreq(self.f.shape[0])
# zero-padded Fourier space function
self.f_pad = np.zeros((self.f.shape[0]-1)*upsample_factor, dtype='complex')
self.f_pad[0:self.f.shape[0]//2] = self.f[0:self.f.shape[0]//2]
self.f_pad[1-self.f.shape[0]//2:] = self.f[1-self.f.shape[0]//2:]
# End point of padded Fourier space function
self.f_pad[self.f.shape[0]//2] = self.f[self.f.shape[0]//2] * 0.5
self.f_pad[-self.f.shape[0]//2] = np.conj(self.f[self.f.shape[0]//2]) * 0.5
# Real space
self.r = np.linspace(0.0,1.0,self.f_pad.shape[0])
f_rs = np.fft.ifft(self.f_pad) * self.f_pad.shape[0]
self.f_real = np.real(f_rs)
self.f_imag = np.imag(f_rs)
self.f_abs = np.abs(f_rs)
self.f_phase = np.angle(f_rs * np.exp(1j*1e-8))
def update_plot(self,f):
"""
Update the plots
"""
# Calculate plotting functions
self.calc_inv_transform(f)
# FFT plots
mag = np.abs(self.f)
phase = np.angle(self.f)
phase_c = cm.hsv(np.mod(phase/(2*np.pi),1.0))
self.p.set_offsets(np.vstack((self.q,mag)).T)
self.p.set_edgecolor(phase_c)
seg_old = self.p_lines.get_segments()
seg_new = [np.array([[qq,0],[qq,mm]]) for mm,qq in zip(mag,self.q)]
self.p_lines.set_segments(seg_new)
self.p_lines.set_color(phase_c)
# real / imag
self.p_real[0].set_xdata(self.r)
self.p_real[0].set_ydata(self.f_real)
self.p_imag[0].set_xdata(self.r)
self.p_imag[0].set_ydata(self.f_imag)
# amp / phase
self.p_abs[0].set_xdata(self.r)
self.p_abs[0].set_ydata(self.f_abs)
self.p_phase[0].set_xdata(self.r)
self.p_phase[0].set_ydata(self.f_phase)
# default function is a cosine wave
f = np.zeros(16, dtype='complex')
f[2] = 1.0
f[0] = 0.001
f[-2] = 1.0
# fft = FourierTransform1D(f)
# # initialize plot
# out = Output(layout=Layout(width='400px',height='300px'))
out = Output()
# display(out)
with out:
fft = FourierTransform1D(f);
# interactive movement of points - store variables inside fft
fft.point_ind = None
fft.qx_init = 0.0
fft.phase_init = 0.0
fft.dphase_dq = (2*np.pi) / 1.0
def button_press_callback(event):
# mouse button pressed
# if left click and within axes, proceed with mouse movement event
if event.inaxes is None:
return
if event.button != 1:
return
# convert from screen coordinates to axis coordinates
t = fft.ax_FFT.transData.inverted()
qx_mag = t.transform([event.x,event.y])
# determine closest point and initial phase of point
fft.point_ind = np.argmin(np.abs(fft.q - qx_mag[0])).astype('int')
fft.qx_init = qx_mag[0]
fft.phase_init = np.angle(fft.f[fft.point_ind])
def motion_notify_callback(event):
# during mouse movement
if fft.point_ind is None:
return
if event.inaxes is None:
return
if event.button != 1:
return
# get point in axis coordinates
t = fft.ax_FFT.transData.inverted()
qx_mag = t.transform([event.x,event.y])
# # # Check if user dragged point outside FOV
# if qx_mag[1] < -0.1 or qx_mag[1] > 1.1:
# fft.point_ind = None
# button_release_callback(event)
# relative q value
dq = qx_mag[0] - fft.qx_init
phase_new = fft.phase_init + dq * fft.dphase_dq
# update fft point
fft.f[fft.point_ind] = np.maximum(qx_mag[1], 0.0) * np.exp(1j*phase_new)
fft.update_plot(fft.f)
def button_release_callback(event):
# mouse button released
if event.button != 1:
return
fft.point_ind = None
# button callbacks
fft.fig.canvas.mpl_connect('button_press_event', button_press_callback)
fft.fig.canvas.mpl_connect('button_release_event', button_release_callback)
fft.fig.canvas.mpl_connect('motion_notify_event', motion_notify_callback)
# Appearance
fft.fig.canvas.resizable=False
fft.fig.canvas.toolbar_visible = False
fft.fig.canvas.header_visible = False
fft.fig.canvas.footer_visible = False
fft.fig.canvas.layout.width = '680px'
# List of options
option_list = (
'cosine wave',
'sine wave',
'plane wave',
'complex wavepacket',
'complex tighter wavepacket',
'real wavepacket - zero mean',
'real wavepacket - positive',
'atoms - 2',
'atoms - 3',
'atoms - 4',
)
# update the plots with a pre-selected function
def select_preset_eventhandler(change):
f = np.zeros(16, dtype='complex')
if change.new == option_list[0]:
# cosine wave
f[ 2] = 1.0
f[-2] = 1.0
elif change.new == option_list[1]:
# sine wave
f[ 2] = -1j*1.0
f[-2] = 1j*1.0
elif change.new == option_list[2]:
# plane wave
f[ 3] = 1j*1.0
elif change.new == option_list[3]:
# complex wavepacket
f[ 5] = -1.0
f[ 6] = 1.0
elif change.new == option_list[4]:
# complex tighter wavepacket
f[ 4] = 0.5
f[ 5] = -1.0
f[ 6] = 1.0
f[ 7] = -0.5
elif change.new == option_list[5]:
# wavepacket - zero mean
f[ 7] = 0.5
f[-8] = -1.0
f[-7] = 0.5
elif change.new == option_list[6]:
# wavepacket - all positive values
f[-7] = -0.25
f[-8] = 0.5
f[ 7] = -0.25
f[-1] = -0.4
f[ 0] = 1.0
f[ 1] = -0.4
elif change.new == option_list[7]:
# atoms - 2
f[-8] = 0.25
f[-6] = 0.25
f[-4] = 0.50
f[-2] = 0.75
f[ 0] = 1.01
f[ 2] = 0.75
f[ 4] = 0.50
f[ 6] = 0.25
elif change.new == option_list[8]:
# atoms - 3
f[-6] = 0.33
f[-3] = 0.66
f[ 0] = 1.01
f[ 3] = 0.66
f[ 6] = 0.33
elif change.new == option_list[9]:
# atoms - 4
f[-8] = 0.5
f[-4] = 0.5
f[ 0] = 1.01
f[ 4] = 0.5
# apply update to plot
fft.update_plot(f)
# Widgets
dropdown = Dropdown(
options = option_list,
layout = Layout(width='200px',height='30px'),
)
dropdown.observe(select_preset_eventhandler, names='value')
# widget layouts
widget = VBox([
HBox([
VBox([
Label('Left click and drag Fourier space samples to change them.',
layout=Layout(width='400px',height='30px')),
Label('up/down - change magnitude. left/right - change phase.',
layout=Layout(width='400px',height='30px')),
]),
VBox([
Label('Preset Functions:',
layout=Layout(width='175px',height='30px')),
dropdown
])
]),
out,
]);
display(widget); VBox(children=(HBox(children=(VBox(children=(Label(value='Left click and drag Fourier space samples to change …