Translationally Invariant VAE
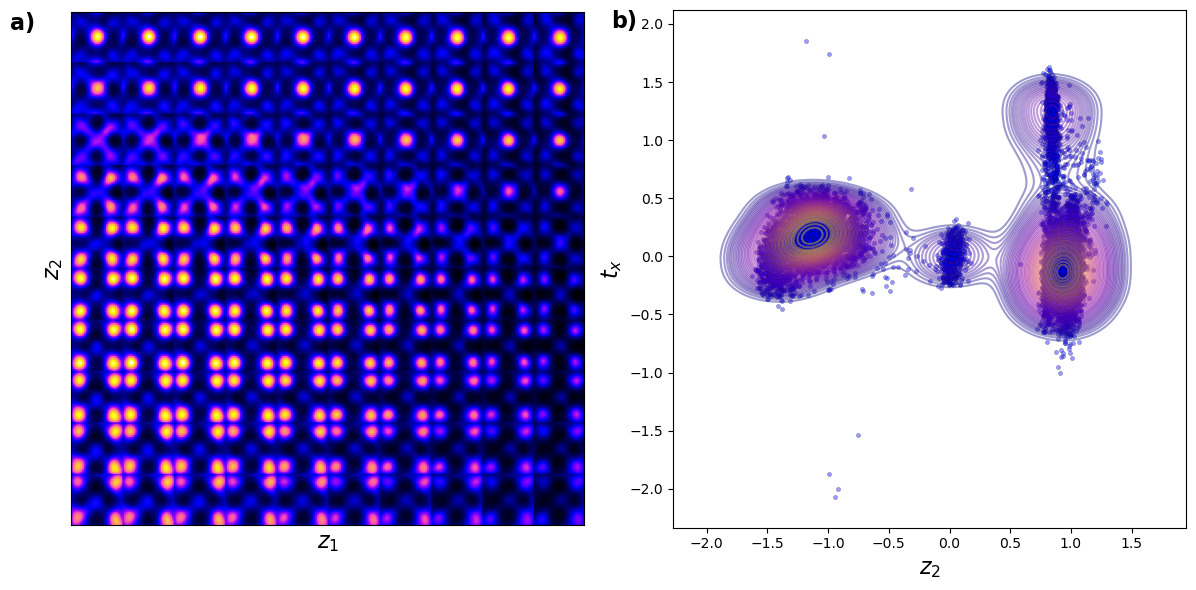
In this approach, the latent space is composed of the intrinsic latent variables along with two additional components representing the translation vector (, ). As a result, the dimensionality of the latent space becomes , where corresponds to the number of intrinsic latent variables. This framework allows us to disentangle and analyze both the intrinsic factors of variation and the translational symmetry within the data.
We observe well-defined clusters, which strongly suggest the presence of underlying physical principles governing the system.
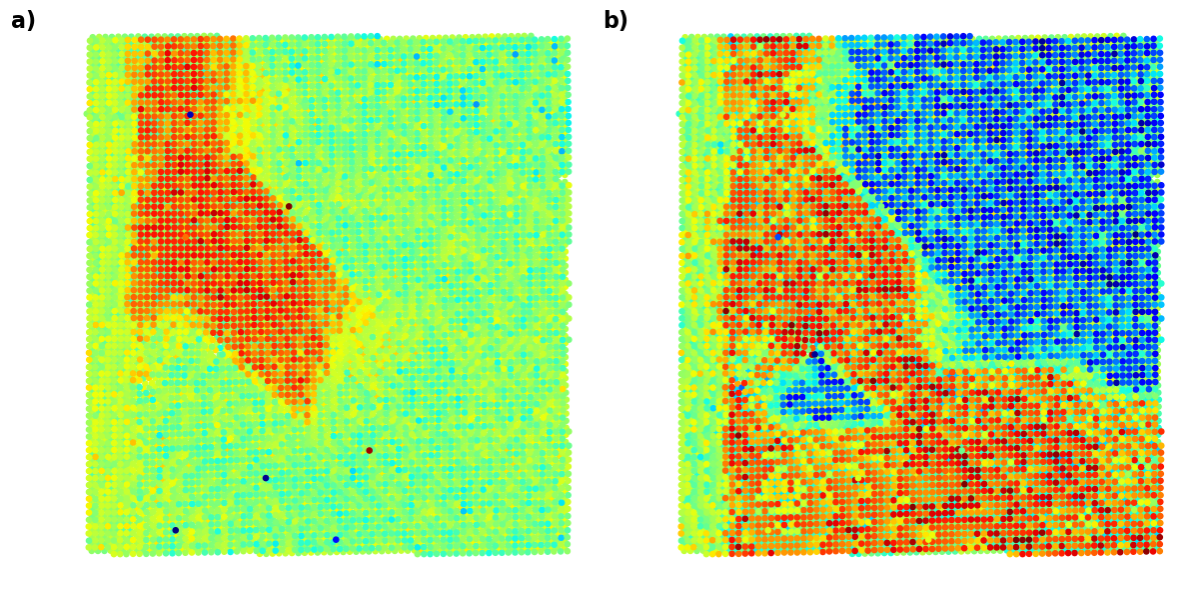
The latent maps reveal fascinating insights. The translation vectors closely resemble the polarization components, aligning with the underlying physics of ferroelectrics, where the polarization arises from the shift of the central atom relative to the corner atoms. Simultaneously, the intrinsic latent variables , and exhibit chemical contrast and mistilt effects, with minor leakage of polarization information into their representation.